Data Analysis
Unit
Director
Dr Guillermo Ortega Rabbione
Address
C/ Diego de León 62 – 7ª planta del Hospital.
28006 Madrid, Spain
Telephone
+34 91 520 22 00 Ext: 17304/17305
guillermojose.ortega@salud.madrid.org
The Data Analysis Unit (UAD) at the Instituto de Investigación Sanitaria (Health Research Institute), Hospital de la Princesa (IIS-IP) aims to provide support, advice and active collaboration to basic and clinical researchers in numerical analysis and data display in biological fields.
It acts as a “first consultation” and advice service on many issues, as well as offering concrete support in the fields in which we have the most proven experience. Due to the high degree of computerisation in all medical areas, such as medical records, recordings through external, internal or portable temporary monitors, sequencing, etc., tools and methods specially designed to process ever-increasing amounts of data must be used.
For all these reasons, the UAD is key to the development of our centre’s research projects, in many cases multidisciplinary, multi-centre, national or international projects.

Dr. Guillermo J. Ortega
Doctor of Physics
Dr. Ancor Sanz-García
Doctor of Neuroscience
Computers
The Unit currently has workstations equipped for high-performance intensive numerical calculations (a Hewlett Packard Z600 server and a workstation with 10 cores, 128 GB of RAM memory and an 11 GB NVIDIA GTX 1080 Ti graphics card, which can be used for GPU-based calculations).
Storage
The Unit has storage for up to 80 TB, which makes it particularly suited to processing large amounts of bioinformatics data, especially data obtained through next-generation sequencing (NGS).
- Time series analysis of biophysical systems
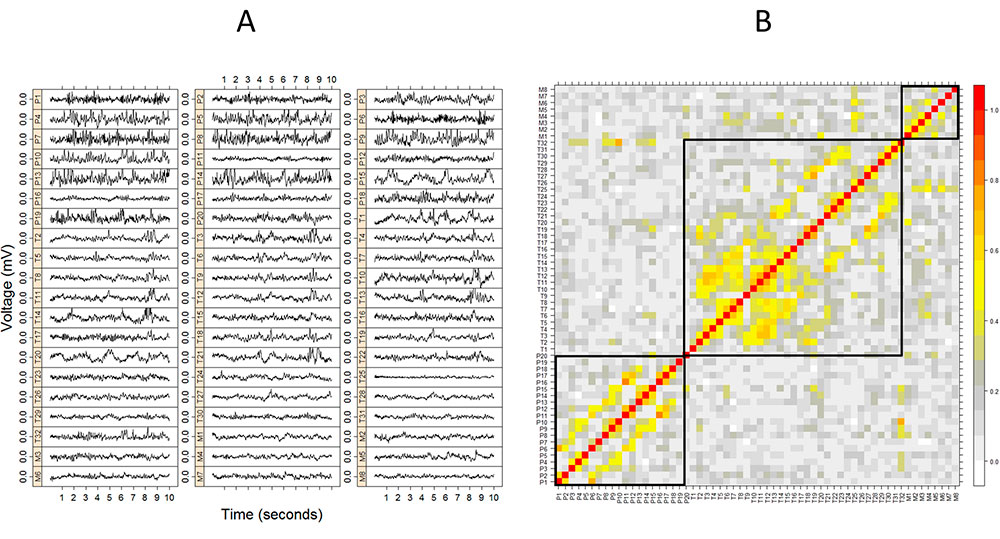
- Mass analysis of multi-modal neurophysiological recordings (EEG, EKG, PIC, etc.)
- Analysis by means of chaos theory in telemetric recordings of body temperature and activity in animal models (hamsters, rats, etc.)
- Time series analysis of spikes from extracellular multi-electrode recordings. Neural code
- Analysis and classification of cellular images using multi-fractal methods
- Biophysical models of cellular communication through gap-junctions
- Biophysical modelling of excitable tissues
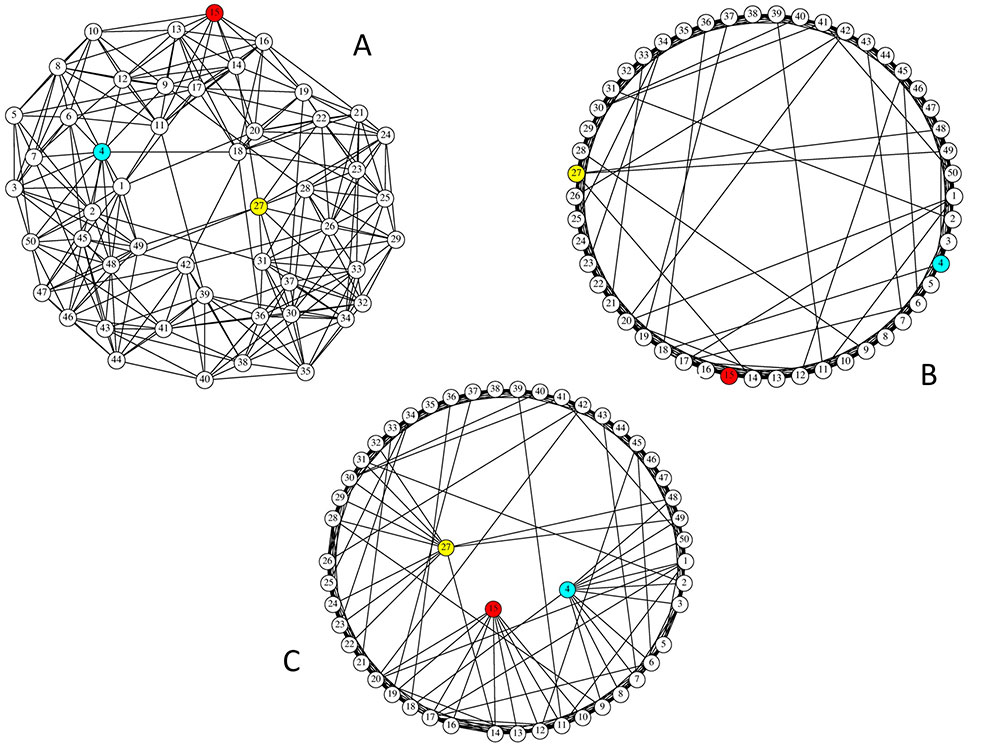
- Use of complex network theory to study human physiological recordings
- Development of time series analysis methods based on chaos theory
- Implementation of machine learning techniques
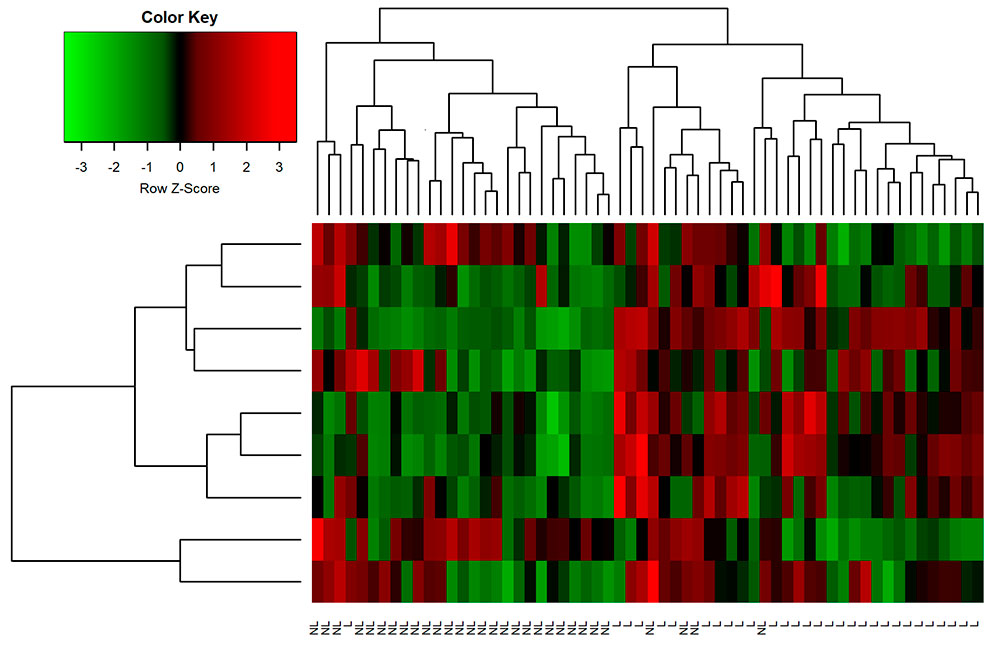
- Development of algorithms for data normalisation in miRNA expression analysis
- Development of programs for the analysis of DNA methylation microarrays
- Analysis of data from mass sequencing, specifically quality control programs.
- Display methods of complex networks
- Management of various programming languages (R, Fortran, python, shell scripting, etc.) and operating systems (Windows, Unix)
- Various data mining techniques
Representative publications in different thematic areas:
Non-invasive monitoring of intracranial pressure
- Sanz-Garcia et al. (2018) Identifying causal relationships between EEG activity and intracranial pressure levels in neurocritical care patients. J Neural Eng.
Epilepsy
- Sanz-Garcia et al. (2017) Towards Operational Definition of Postictal Stage: Spectral Entropy as a Marker of Seizure Ending. Entropy. 19:81.
- Sanz-Garcia et al. (2016) Network Analysis of Foramen Ovale Electrode Recordings in Drug-resistant Temporal Lobe Epilepsy Patients. J. Vis. Exp. 118:e54746.
- Vega-Zelaya L et al. (2016) Assessing the equivalence between etomidate and seizure network dynamics in temporal lobe epilepsy. Clin Neurophysiol. 127:169-178.
- Vega-Zelaya L et al. (2015) Disrupted Ipsilateral Network Connectivity in Temporal Lobe Epilepsy. PLoS One. 10:e0140859.
- Palmigiano A et al. (2012) Stability of Synchronization Clusters and Seizurability in Temporal Lobe Epilepsy. PLoS One 7:e41799.
- Ortega GJ et al. (2011) Impaired mesial synchronization in temporal lobe epilepsy. Clin Neurophysiol. 122:1106-1116
- Ortega GJ et al. (2008) Synchronization clusters of interictal activity in the lateral temporal cortex of epileptic patients: Intraoperative electrocorticographic analysis. Epilepsia 49:269-280
Epigenetics
- Ovejero-Benito et al. (2018) Epigenetic biomarkers associated with anti-TNF drugs response in moderate-to-severe psoriasis. Br J Dermatol. 178:798-800.
miRNAs
- Martínez-Hernández et al. (2018) A microRNA signature for evaluation of risk and severity of Autoimmune Thyroid Diseases. J Clin Endocrinol Metab. 103:1139-1150.
Time series analysis of spikes from extracellular multi-electrode recordings
- Ortega GJ et al. (2004) Conditioned Spikes: A simple and fast method to represent rates and temporal patterns in multielectrode recordings. J of Neurosci Methods 133:135-141.
Analysis and classification of cellular images using multi-fractal methods
- Fernandez E et al. (1999) Are Neurons Multifractals? J Neurosci Methods 89:151.
Biophysical models
- Boschi CD et al (2001) Triggering synchronized oscillations through arbitrarily weak diversity in close-to-threshold excitable media. Phys Rev E 63:12901
Andreu E et al. (2000) Role of Architecture in Determining Passive Electrical Properties in Gap-Junction Connected Cells. Pflügers Arch – Eur J Physiol 439:789-97
Development of time series analysis methods based on chaos theory
- Ortega G et al. (1998) Smoothness Implies Determinism in Time Series: A Measure Based Approach. Phys Rev Lett 81:4345.
TARIFAS
| PERSONAL IISHUP | PERSONAL EXTERNO | |
|---|---|---|
| Consultas sin análisis numérico | Gratuito | 30 €/hora |
| Consultas con análisis numérico | 21€/hora | 50€/hora |
| Asesoría proyectos (con análisis numérico y/o elaboración informes) | 27 €/hora | 70 €/hora |
| Formación/Cursos (R, Linux, Machine Learning) | 50 €/hora | 80 €/hora |
| Desarrollo de scripts | 30 €/hora | 70 €/hora |
| Uso de recursos informáticos (estación de trabajo, software) | 100 €/año | 400 €/año |
Modelo Numérico de propagación de COVID-19 en la Comunidad de Madrid. Posibles escenarios para distintos tipos de intervenciones no-farmacológicas y tipos de desescaladas
La Unidad de análisis de Datos del IIS del Hospital de la Princesa ha desarrollado un modelo de análisis epidemiológico compartimental que permite estudiar la evolución de los distintos estados de la población de la comunidad de Madrid ante varios escenarios. El método tiene en cuenta a la población general dividida en los siguientes compartimientos:
- (S) Susceptibles: Aquellas personas susceptibles de contraer la enfermedad COVID-19 pero que todavía no han sido contagiados.
- (I) Infectados: Aquellas personas que ya han sido contagiadas con síntomas “leves” y por lo tanto no requieren hospitalización.
- (H) Hospitalizados: Aquellas personas que por su evolución del COVID-19 necesitan ser hospitalizados.
- (SC) Susceptibles en Cuarentena: Parte de la población de Susceptibles que se encuentran en cuarentena y por lo tanto está “protegida” de contraer la enfermedad.
- (IC) Infectados en Cuarentena: Parte de la población de Infectados que se encuentran en cuarentena y por lo tanto no transmiten la enfermedad
- (RC) recuperados en Cuarentena: Parte de la población de recuperados que se encuentran en cuarentena.
- (M) Muertes: Número de personas que han fallecido debido al agravamiento de la enfermedad
- (R) Recuperados: Aquellas personas que se han recuperado satisfactoriamente del COVID-19
No se ha tenido en cuenta un compartimiento para Expuestos, esto es, contagiados asintomáticos que no transmiten la enfermedad, ya que en el caso de infecciones por SARS-CoV-2 es muy probable que el pico de “contagiosidad” de los infectados se encuentra antes de que comiencen los síntomas [1]. Por lo tanto hemos considerado que todos los contagiados son contagiosos.
Debido a estos compartimentos, hemos llamado al modelo SIHCMR. además, el modelo permite estudiar la dinámica de interacción entre los compartimientos en distintas poblaciones, las cuales no se encuentra aisladas, sino que, por el contrario, pueden intercambiar personas en algunos de los estados S, I y R.
El modelo ha sido desarrollado en R sobre la base del paquete R SimInf [2].
El siguiente grafico muestras posibles “transiciones” que pueden aparecer a lo largo de la evolución de contagio en una población determinada.
[1] Temporal dynamics in viral shedding and transmissibility of COVID-19. (2020) Nature medicine, 26(5), 672-675. [2] Journal of Statistical Software November 2019, Volume 91, Issue 12. doi: 10.18637/jss.v091.i12 Puesto que el modelo permite estudiar tanto las transiciones entre compartimientos como así también el flujo de personas, transmisoras de la enfermedad entre distintas regiones, un esquema mas completo del modelo es el que se muestra en la siguiente Figura, en donde el flujo de personas que pueden estar en los estados S, I o R pueden moverse entre municipios.
Puesto que el modelo permite estudiar tanto las transiciones entre compartimientos como así también el flujo de personas, transmisoras de la enfermedad entre distintas regiones, un esquema mas completo del modelo es el que se muestra en la siguiente Figura, en donde el flujo de personas que pueden estar en los estados S, I o R pueden moverse entre municipios.

De acuerdo a lo anterior por tanto es posible estudiar diversas situaciones a las cuales puede enfrentarse la Comunidad de Madrid y de esta forma evaluar la mejor estrategia no farmacológica a implementar, de tal forma que el costo social y sanitario sea el menor posible.
A modo de ejemplo se muestran algunos casos de “prueba”
Ejemplo 1: Inicio de la epidemia de COVID-19 en Madrid, sin cuarentena. 5 casos iniciales
Parámetros
Datos modelo COVID-19:
β (tasa de transmisión)= 0.14
γ (tasa de recuperación)=0.05
Inicialmente sin Hospitalizado, ni Cuarentena ni Muertos, esto es, Modelo SIR con transferencias de personas entre Municipios
Datos Madrid: Poblaciones de los distintos municipios de la Comunidad de Madrid
Flujo de personas: 5% de poblaciones cercanas se desplazan (ida y vuelta en el día) entre poblaciones de mas de 30.000 habitantes
En esta figura se muestra la evolución de los compartimentos para el caso de una evolución “libre” sin que exista ninguna intervención como cuarentena y/o distanciamiento, ni muertos ni hospitalizados
Se muestra la evolución para los 9 municipios de Madrid de mas de 30.000 habitantes.
En todos los casos existe un movimiento de personas entran/salen de cada municipio con los vecinos, de un 5%.
El comienzo de la infección es en Madrid con 5 casos. La línea punteada marca el momento del máximo de infecciones en Madrid ciudad.
Se ve que en todos los municipios grandes, salvo en Alcobendas, el pico de infecciones se encuentra tanto antes como después del de Madrid.

Ejemplo 2: Inicio de la epidemia de COVID-19 en Madrid, con 150 días de cuarentena. 5 casos iniciales
Movilidad en la Comunidad de Madrid
El Instituto Nacional de Estadísticas (INE) ha hecho público los datos de movilidad de España, tomados del 80% de los teléfonos móviles de los tres principales operadores de teléfono móvil (Orange, Telefónica, Vodafone). Esto permite estudiar como es el flujo de personas entre las distintas localidades. Para su estudio, el país está dividido en “celdas” y el tránsito de las personas se cuantifican de acuerdo con el pasaje de las señales de los móviles de unas celdas a otras. El INE ha hecho publico estos datos entre las distintas celdas de España en el periodo de “estado de alarma”, del 15 de marzo al 20 de junio de 2020 con datos (casi) diarios. Estos datos muestran tanto el flujo de personas “salientes” de una celda como las “entrantes” en el mismo día. Esto permite por lo tanto estudiar como el flujo de personas afecta a la propagación de la epidemia. Además, ha publicado como referencia, un promedio de la movilidad en España en una semana típica de noviembre de 2019.
En nuestro modelo hemos seleccionado las celdas correspondientes a la Comunidad de Madrid, 293 y estudiado el flujo de personas entrantes/salientes de cada una de las celdas durante el estado de alarma.
Con el objeto de introducir la movilidad de las personas en el modelo, y para contar con datos de transito en tiempos normales, hemos generado, a partir de los datos de noviembre de 2019, 500 “días” mas, generando valores subrogados (resampleados) a partir de los datos originales. Esto no permite estudiar la evolución de la epidemia en tiempos fuera del periodo del estado de alarma.

Esta figura muestra el movimiento de personas en un día “normal” para 3 celdas, Pozuelo de Alarcón (distrito 01) en azul, Colmenarejo en verde, y Madrid (Aplomeras Sureste-1). En el grafico se observa a cada región de referencia en negro, y en los respectivos colores hacia dónde va la población residente de cada una. El movimiento de la población se muestra en porcentajes de la población total de cada celda.

En esta figura se muestra lo mismo que en la anterior pero para el caso del periodo del estado de alarma, donde ese observa la drástica reducción en la movilidad de las personas.
Modelo completo con movilidad de personas
El paso siguiente ha sido incluir la movilidad de las personas, cuantificado con los datos del INE, esto es, tener en cuenta todos los compartimentos S, I, R, H, M, QS, QI, QR para cada una de las celdas y teniendo en cuanta el flujo, entrante y saliente, de personas en cada celda con los respectivos destinos.
Una simulación de esto para el caso de los datos “reales” es la que se puede ver en la figura de abajo.

En este caso la dinámica de la epidemia ha comenza con 5 casos en una celda particular al tiempo 0. Se representa la evolución en 9 celdas particulares de la Comunidad de Madrid. Se puede observar que al tener en cuenta el movimiento de las personas, las curvas dejan de ser “suaves”. La línea de color negro representa el número de infectados en cada celda. Al día 170 y debido a la cantidad de infectados se determina una “cuarentena” del 50% de la población,
lo que incluye a los S, I y R y que dura hasta el día 200 (30 días de aislamiento) . La figura de abajo muestra en más detalle el periodo de cuarentena.

Para el caso de las personas hospitalizadas y muertes (D), se puede observar en la siguiente figura la evolución para cada una de las celdas graficadas.

Evolución de la epidemia en la Comunidad de Madrid con el modelo completo Para tener una idea de como evoluciona la epidemia, para estos parámetros del modelo y en esta situación simulada de periodos de no-confinamientos, tenemos la figura siguiente, en donde se muestra el porcentaje de infectados, respecto de la celda correspondiente, para todas las celdas de la Comunidad de Madrid, de acuerdo al modelo anterior.

En el caso que interés el numero de hospitalizados previstos en función del tiempo, podemos observar esta situación en el gráfico de abajo. Tener en cuanta que el modelo llama “hospitalizados” a las personas que necesitan atención en las Unidades de Cuidados Intensivos.

Estudios actuales de estrategias de mitigación en la Comunidad de Madrid. Casos de rebrotes y olas sucesivas de contagios
Muchos de los modelos actuales de COVID-19 prevén una segunda “ola de contagios” pasada la inicial y en otros escenarios, varias olas sucesivas [3], por lo que es necesario desarrollar estrategias de prevención
Actualmente estamos trabajando con el modelo estudiando distintas situaciones de interés para la sanidad publica de Madrid, con datos reales de la cobertura sanitaria del área única de la comunidad de Madrid y de los 262 Centros de Salud de atención primaria asociados a cada uno de los 11 sectores en que se divide esta. El trabajo tiene en cuenta la población asignada a cada C.S. por tramos etarios y factores de riesgo para COVID-19 –diabetes, obesidad, EPOC, etc.-
En este entorno, se están estudiando los siguientes posibles escenarios para el caso de la “segunda ola” y sucesivas olas de contagios.
- Estimación de los parámetros reales del modelo (b, g, a, d) SIHCMR para la comunidad de Madrid.
- Estrategias de Mitigación en la comunidad de Madrid (I): Efectos de las cuarentenas, optimización del periodo de días de la cuarentena y porcentaje de la población de susceptibles.
- Estrategias de Mitigación en la comunidad de Madrid (II): Efectos de medidas de distanciamiento y sanitarias en la población de Madrid.
- Estrategias de Mitigación en la comunidad de Madrid (III): Compartimentalización de municipios, aislamiento de poblaciones de riesgo.
- Determinar la “inmunidad de rebaño” para cada población en determinadas condiciones.
Bibliografía consultada (parte)
- SimInf: An R package for Data-driven Stochastic Disease Spread Simulations
- Data-based analysis, modelling and forecasting of the COVID-19 outbreak
- Improved inference of time-varying reproduction numbers during infectious disease outbreaks
- Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2)
- Temporal dynamics in viral shedding and transmissibility of COVID-19
- Methods for estimating disease transmission rates: Evaluating the precision of Poisson regression and two novel methods
- A mathematical description of the dynamics of coronavirus disease 2019 (covid-19): a case study of brazil
- Hospitalization Rates and Characteristics of Patients Hospitalized with Laboratory-Confirmed Coronavirus Disease 2019 — COVID-NET, 14 States, March 1–30, 2020
- Early dynamics of transmission and control of COVID-19: a mathematical modelling study
- Common trends in the epidemic of Covid-19 disease
- Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts
- Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia
- Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2)
- The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak
- COVID-19: The CIDRAP Viewpoint: Part 1: The Future of the COVID-19 Pandemic: Lessons Learned from Pandemic Influenza
- Estimates of the severity of coronavirus disease 2019:a model-based analysis